Arbitrary Precision using Python Mpmath

Mpmath is great, powerful and easy to use to calculating equation that involve floating point.
I found several article that could be used to find minimal setting for arbitrary precision, enough the chat, let my code do the talk..

Software that used:

• python ver 2.6.5 in ubuntu 10.04 64 bit
• python EPD(Enthought Python Distribution) ver 7.0-2 32 bit in windows 7 64 bit, no default mpmath installation under python epd, but its available via sympy(included ver 0.14 mpmath)
• python mpmath ver 0.17, http://code.google.com/p/mpmath/
• gmpy -> python binding for GMP
• sage version 4.7 64bit for ubuntu10.04  http://www.sagemath.org/

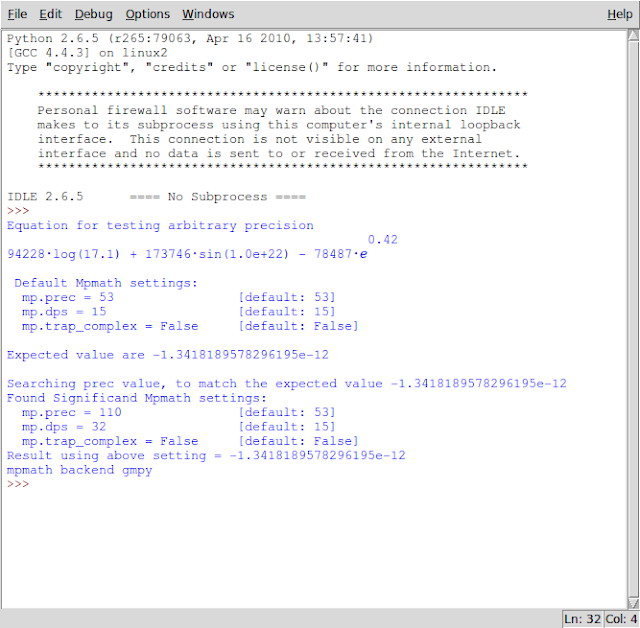
Below are 2 equations that could be used for searching significant setting for mpmath arbitrary precision.
1. Interval Arithmetic: Python Implementation and Applications by Stefano Taschini in SciPy2008_proceedings.pdf
GMPY Backend

SAGE Backend

Python Backend

2. Why and how to use arbitrary precision by Kaveh R. Ghazi, Vincent Lefèvre, Philippe Théveny, Paul Zimmermann in cise.pdf
GMPY Backend

SAGE Backend

Python Backend

Conclusion

• different BACKEND in mpmath did not effect in result and mpmath.mp context(setting for arbitrary precision), just gives an performance effect(sage faster, than gmpy, last python) 
• mpmath prec value that could be gives most precision is not less than 128 bit (mpmath.mp.prec=128)
• creating a mpf object is better to converted into string data type first( mp.mpf('0.1') or mp.mpf(str(0.1)))
• better doing a arithmetic rational operation when possible see first code that solved using sympy